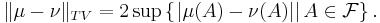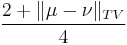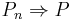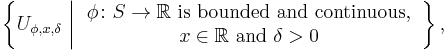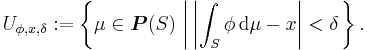Convergence of measures
In mathematics, more specifically measure theory, there are various notions of the convergence of measures. Three of the most common notions of convergence are described below.
Contents |
Total variation convergence of measures
This is the strongest notion of convergence shown on this page and is defined a follows. Let 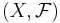 be a measurable space. The total variation distance between two (positive) measures
be a measurable space. The total variation distance between two (positive) measures  and
and  is then given by
is then given by
If  and
and  are both probability measures, then the total variation distance is also given by
are both probability measures, then the total variation distance is also given by
The equivalence between these two definitions can be seen as a particular case of the Monge-Kantorovich duality. From the two definitions above, it is clear that the total variation distance between probability measures is always between 0 and 2.
To illustrate the meaning of the total variation distance, consider the following thought experiment. Assume that we are given two probability measures  and
and  , as well as a random variable
, as well as a random variable  . We know that
. We know that  has law either
has law either  or
or  , but we do not know which one of the two. Assume now that we are given one single sample distributed according to the law of
, but we do not know which one of the two. Assume now that we are given one single sample distributed according to the law of  and that we are then asked to guess which one of the two distributions describes that law. The quantity
and that we are then asked to guess which one of the two distributions describes that law. The quantity
then provides a sharp upper bound on the probability that our guess is correct.
Strong convergence of measures
For  a measurable space, a sequence
a measurable space, a sequence 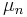 is said to converge strongly to a limit
is said to converge strongly to a limit  if
if
for every set in 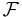 .
.
For example, as a consequence of the Riemann–Lebesgue lemma, the sequence 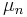 of measures on the interval [-1,1] given by
of measures on the interval [-1,1] given by 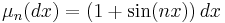 converges strongly to Lebesgue measure, but it does not converge in total variation.
converges strongly to Lebesgue measure, but it does not converge in total variation.
Weak convergence of measures
In mathematics and statistics, weak convergence (also known as narrow convergence or weak-* convergence which is a more appropriate name from the point of view of functional analysis but less frequently used) is one of many types of convergence relating to the convergence of measures. It depends on a topology on the underlying space and thus is not a purely measure theoretic notion.
There are several equivalent definitions of weak convergence of a sequence of measures, some of which are (apparently) more general than others. The equivalence of these conditions is sometimes known as the portmanteau theorem.
Definition. Let S be a metric space with its Borel σ-algebra Σ. We say that a sequence of probability measures on (S, Σ), Pn, n = 1, 2, ..., converges weakly to the probability measure P, and write
if any of the following equivalent conditions is true:
- Enƒ → Eƒ for all bounded, continuous functions ƒ;
- Enƒ → Eƒ for all bounded and Lipschitz functions ƒ;
- limsup Enƒ ≤ Eƒ for every upper semi-continuous function ƒ bounded from above;
- liminf Enƒ ≥ Eƒ for every lower semi-continuous function ƒ bounded from below;
- limsup Pn(C) ≤ P(C) for all closed sets C of space S;
- liminf Pn(U) ≥ P(U) for all open sets U of space S;
- lim Pn(A) = P(A) for all continuity sets A of measure P.
In the case S = R with its usual topology, if Fn, F denote the cumulative distribution functions of the measures Pn, P respectively, then Pn converges weakly to P if and only if limn→∞ Fn(x) = F(x) for all points x ∈ R at which F is continuous.
For example, the sequence where Pn is the Dirac measure located at 1/n converges weakly to the Dirac measure located at 0 (if we view these as measures on R with the usual topology), but it does not converge strongly. This is intuitively clear: we only know that 1/n is "close" to 0 because of the topology of R.
This definition of weak convergence can be extended for S any metrizable topological space. It also defines a weak topology on P(S), the set of all probability measures defined on (S, Σ). The weak topology is generated by the following basis of open sets:
where
If S is also separable, then P(S) is metrizable and separable, for example by the Lévy–Prokhorov metric, if S is also compact or Polish, so is P(S).
If S is separable, it naturally embeds into P(S) as the (closed) set of dirac measures, and its convex hull is dense.
There are many "arrow notations" for this kind of convergence: the most frequently used are 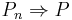 ,
, 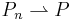 and
and 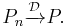 .
.
Weak convergence of random variables
Let 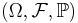 be a probability space and X be a metric space. If Xn, X: Ω → X is a sequence of random variables then Xn is said to converge weakly (or in distribution or in law) to X as n → ∞ if the sequence of pushforward measures (Xn)∗(P) converges weakly to X∗(P) in the sense of weak convergence of measures on X, as defined above.
be a probability space and X be a metric space. If Xn, X: Ω → X is a sequence of random variables then Xn is said to converge weakly (or in distribution or in law) to X as n → ∞ if the sequence of pushforward measures (Xn)∗(P) converges weakly to X∗(P) in the sense of weak convergence of measures on X, as defined above.
References
- Ambrosio, L., Gigli, N. & Savaré, G. (2005). Gradient Flows in Metric Spaces and in the Space of Probability Measures. Basel: ETH Zürich, Birkhäuser Verlag. ISBN 3-7643-2428-7.
- Billingsley, Patrick (1995). Probability and Measure. New York, NY: John Wiley & Sons, Inc.. ISBN 0-471-00710-2.
- Billingsley, Patrick (1999). Convergence of Probability Measures. New York, NY: John Wiley & Sons, Inc.. ISBN 0-471-19745-9.
![\|\mu- \nu\|_{TV} = \sup \Bigl\{\int_X f(x) (\mu-\nu)(dx) \Big| f\colon X \to [-1,1] \Bigr\}.](/2012-wikipedia_en_all_nopic_01_2012/I/7672293ec7ab26734a27dc8c6492c172.png)